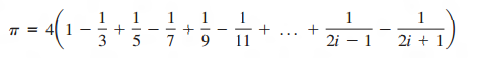JAVA PRACTICE EXAM
Know that how good you are in programming
Problem A [Two’s Power]
Write a program that reads an integer n
and checks whether n is a power of 2 (powers of 2 are 1,2,4,8,16,32, …). The
output of your program is either “yes” or “no”.
public class LAU1
{
public static void main (String[] args)
{
java.util.Scanner scan = new java.util.Scanner(System.in);
int n = scan.nextInt();
while (n >= 2)
{
if(n%2 != 0)
break;
if (n%2 == 0)
n/=2;
}
if (n == 1) System.out.println("yes");
else
System.out.println("no");
}
} |
Problem B [No Duplicates]
Write a program that read a string str
and prints a string obtained from str by removing/ignoring duplicates. For
example, if str is abbacdcae, then your program prints abcde. In other words,
only the first occurrence of a character is printed.
import java.util.Scanner;
public class LAU2
{
public static void main (String[] args)
{
String target = "";
Scanner scan = new Scanner (System.in);
String S = scan.nextLine();
for (int i =0;i<S.length();i++)
{
boolean so = true;
for (int j = 0 ; j<i;j++)
{
if (S.charAt(i) == S.charAt(j))
so = false;
}
if (so) target += S.charAt(i);
}
System.out.print(target);
}
}
|
|
Problem C [Integer Mirror]
Write a program that reads an integer N followed
by N positive integers. For each entered integer, your program prints (on a
new line) its digits in reverse. For example:
Input
3
35423
7
98710789
Output
32453
7
98701789
import java.util.Scanner;
public class LAU3
{
public static void main (String[] args)
{
Scanner scan = new Scanner (System.in);
int N = scan.nextInt();
String[] nums = new String[N];
for (int i =0;i<N;i++)
{
nums[i] = scan.next();
}
for (int i = 0;i<N;i++)
{
for (int j =nums[i].length()-1;j>=0;j--)
{
System.out.print(nums[i].charAt(j));
}
System.out.println();
}
}
}
|
|
Problem D [Prime Frequency]
Write a program that reads positive
integers from the keyboard until the user enters 0. Then the program prints the
number of prime numbers entered. Here is a sample:
public class LAU4
{
public static boolean isPrime(int n)
{
if(n ==0 || n == 1 )
return false;
for (int i =2;i<n;i++)
{
if (n%i == 0)
return false;
}
return true;
}
public static void main (String[] args)
{
java.util.Scanner scan = new java.util.Scanner(System.in);
int i = -1;
int count = 0;
while ( i != 0)
{
i = scan.nextInt();
if (isPrime(i)) count++;
}
System.out.println(count);
}
}
|
|
Problem E [Palindromes]
Write a program that reads an integer
N followed by N strings. For each string, your program prints yes or no
according whether the string is a palindrome or not. Here is a sample:
3
kayak yes
palindrome no
wow yes
Input Output
public class LAU5
{
public static boolean isPalindrome(String str)
{
for (int i = 0;i<str.length()-1;i++)
{
if (str.charAt(i) == str.charAt(str.length()-1-i))
return true;
}
return false;
}
public static void main (String[] args)
{
java.util.Scanner scan = new java.util.Scanner(System.in);
int N = scan.nextInt();
for (int i =0;i<N;i++)
{
String temp = scan.next();
if (isPalindrome(temp)) System.out.println("yes");
else
System.out.println("no");
}
}
}
|
|
Problem F [Flipped Star Triangles]
Complete the following program by
writing the method starTriangle that takes an integer i and draws a flipped triangle
(as shown below) of height i that is filled with stars. The main method (below)
calls starTriangle N times, each time with one of the numbers between 1 and N. For
example, if N is 3, the program calls starTriangle 3 times and prints:
*****
***
*
public static void main(String[] args) {
Scanner
input = new Scanner(system.in);
int N = input.nextInt();
for(int i = 1; i <= N; i++){
starTriangle(i);
System.out.println();
}
}
Problem G [Fibonacci Number]
Complete and submit the following
program by writing the boolean method isFib, which takes a positive integer n
and checks whether n is one of the Fibonacci numbers (1,1,2,3,5,8,13,…).
public class FibNum
Input Output
3
2 yes
10 No
13 Yes
|
|
{
public static boolean isFib(int n)
{
}
public static void main(String[] args)
{
Scanner input = new Scanner(System.in);
int n, testnums = input.nextInt();
for(int j = 1; j <= testnums; j++)
{
n = input.nextInt();
if(isFib(n))
System.out.println(“Yes”);
else System.out.println(“No”);
}
}
}
import java.util.Scanner;
public class LAU7
{
public static boolean isFib(int n)
{
int a = 1;
int b =1;
int c = 0;
for (int i = 0;c<=n;i++)
{
c = a+b;
a = b;
b = c;
if (c==n)
return true;
}
return false;
}
public static void main(String[] args)
{
Scanner input = new Scanner(System.in);
int n, testnums = input.nextInt();
for(int j = 1; j <= testnums; j++)
{
n = input.nextInt();
if(isFib(n))
System.out.println("Yes");
else System.out.println("No");
}
}
} |
Problem H [Longest Natural
Successors]
Two consecutive integers are natural
successors if the second is the successor of the first in the sequence of
natural numbers (1 and 2 are natural successors). Write a program that reads a
number N followed by N integers, and then prints the length of the longest
sequence of consecutive natural successors. Example:
Input Output
7 2 3 5 6 7
9 10 3